Research on active debris removal is essential for maintaining space sustainability. By developing technologies to eliminate space junk, we can prevent collisions that endanger satellites and space missions. Effective debris removal ensures the safety and longevity of space operations, supports future exploration, and protects valuable assets in Earth’s orbit.
Active Debris Removal (ADR)
Relative Pose Estimation
Spacecraft relative state estimation is of paramount importance in the problem of rendezvous with an uncooperative target; indeed, an accurate prediction of its relative position and attitude is crucial for safe proximity operations, especially considering autonomous guidance, navigation, and control. Therefore, a key point for the success of these missions is the development of efficient algorithms capable of limiting the computational burden without any reduction in performance. Our research addresses the issue proposing and analyzing nonlinear filters based on differential algebra. High-order numerical extended Kalman filter and unscented Kalman filter are developed in the differential algebra framework, and their performance is assessed and compared in terms of accuracy, robustness, and computational time, highlighting advantages and drawbacks. The European Space Agency e.deorbit mission, involving Envisat, is
considered as the reference case, and the analysis is carried out through numerous numerical simulations, taking into account different measurement acquisition frequencies and levels of uncertainties.
Using Differential Algebra, Dr. Servadio created the UKFDA and the EKFDA to estimate the relative pose between a chaser spacecraft and the uncontrolled derelict Envisat with high accuracy. The following video shows the onboard camera of the chaser looking at Envisat, the frequency of pictures taken, and the estimation of relative position, velocity, attitude, and angular velocity.
The filter is based on identifying the corners of the derelict, called markers. Here is an overview of the software architecture that visualizes how the filter works.
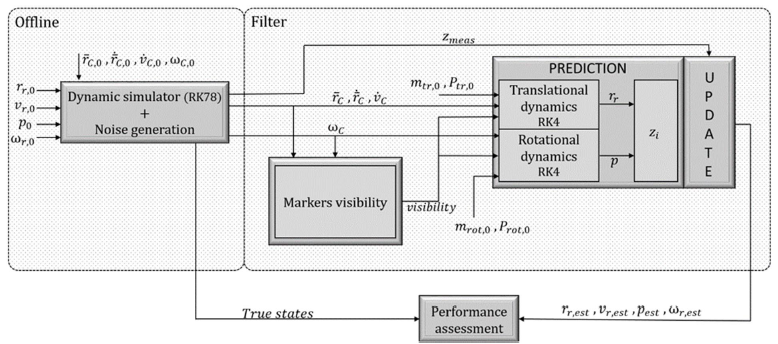
The software architecture is made up of three main blocks. The first one is the “dynamics simulator+noise generator,” which receives as inputs the initial states, then propagates the dynamics through a variable-step integrator (Runge–Kutta 7-8 propagator) and generates the measurements adding noise computed with the exponentially correlated random model. These computations are performed in advance, and the outputs are loaded in memory
before running the filter. For the filtering, the decoupling of the equations of motion can be exploited to separate the propagation of the two dynamics, translational and rotational, leading to a faster and more efficient algorithm. In this case a fixed-step integrator is used, because it is computationally
lighter. On the other hand, as regards the estimation of the measurements, the translational and rotational information has to be used jointly, because the measurement equations are coupled. The filter is initialized providing an initial estimate of the relative states in terms of mean and covariance. Moreover, before starting the estimation, the filter uses the information from the previous step to calculate the marker’s visibility. Finally, the estimated relative state is compared with the true state propagated by the dynamics simulator to assess the performance of the filters.
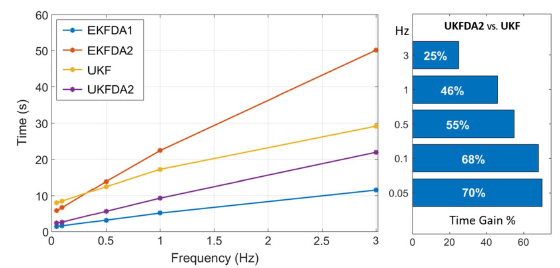
UKF (right).
The graph in the figure (left) is a graphical representation of the computational time behavior of the filters at different frequencies in the case where all the
visible markers are used as measurements. The linear filter EKFDA1 is the fastest one. The EKFDA2 is the filter with the most demanding computational time at high frequency, but it is faster than the standard UKF at a very low frequency. The UKFDA2 has nearly the same trend as the UKF but requires less time. Therefore, the improvement of including DA in the UT is evident: the two filters have the same accuracy, but the one based on DA is faster in the whole frequency range. The histogram in the figure (right) emphasizes the computational advantage gained by the DA implementation of the UKF. Each bar represents the percentage of workload saved by the UKFDA2 (over the UKF) during all the prediction steps, for each simulation at different acquisition frequencies.
Target Selection and Risk Index
The first step of any active debris removal (ADR) mission is the selection of the target. The optimal choice is to find the most dangerous debris that can be removed considering the chaser spacecraft requirements and mission constraints. After creating a catalog of the current space population in low Earth orbit (LEO), the MIT Monte Carlo Orbital Capacity Assessment Tool (MOCAT-MC) is used to simulate and predict the future space environment and the interaction among the space population. A novel performance index to quantify the criticality of each debris and the risk that it presents to the space environment is proposed. The new risk index considers the proximity of the debris to highly populated regions, its persistence in orbit, its likelihood to collide, and the estimated number and mass of debris that it can generate. The risk index is then optimized to work either with the full space population or a subset of it, where the ranking of risk among debris is highlighted. Multiple risk analyses are proposed in the test cases, where the ranked list of optimal targets is provided
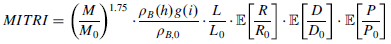
MITRI is a performance index optimized to work on subregions of the LEO environment, as it underlines differences among the debris that score similarly and orbit one close to the other. However, it is possible to select the LEO space environment as a whole and provide the overall most dangerous debris orbiting the Earth. That is, the domain selected for the MITRI evaluation considers every (uncontrolled) RSO.
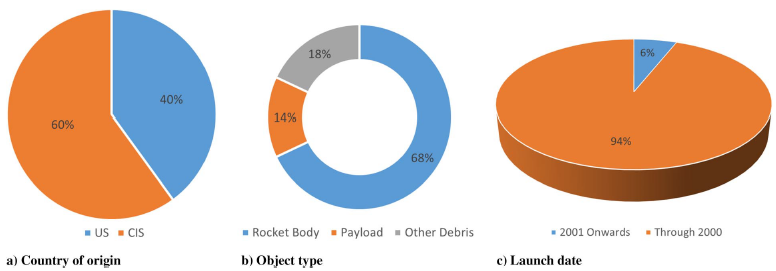
Dr. Servadio developed the MITRI risk index to rank the most dangerous debris orbiting in LEO following the results and simulations from MOCAT-MC. Whenever analyzing the nature of these highly ranked RSOs, the above figure shows that they are human-made debris, with origin either Russian or
American (a). As expected, most of them are massive rocket bodies, while the remainder are derelict satellites that never had or failed their PDM (b). Indeed, these debris date back before to the year 2001, when mitigation guidelines were not yet mandatory, or they got abandoned before mitigation guidelines were established (c).
Policy and Economic Factors
This section will be added after the research will be presented at the upcoming STM conference.
